728x90
포물선의 초점을 지나가는 직선의 성질

$$\Box \textrm{ABCD}=(a+b)\sqrt{ab} $$
[증명]

포물선 $y^2 = 4px$ 에서 초점 F를 지나는 직선이 포물선과 만나는 두 점을 A, B라 하고 두 점 A, B에서 준선 $x=-p$ 에 내린 수선의 발을 각각 C, D라 하자.
사다리꼴 ABCD의 넓이는
$\rm \displaystyle\frac{1}{2} \left( \overline{AC}+\overline{BD} \right ) \times \overline{CD} $
$=\displaystyle\frac{1}{2} (a+b) \times 2 \sqrt{ab}$
$=(a+b)\sqrt{ab}$
여기서, $\rm \overline{CD}$ $=2\sqrt{ab}$ 도 자주 사용된다.

| Example 1 |
포물선의 초점을 지나는 직선이 포물선과 만나는 점을 각각 A, B라 하고 두 점 A, B에서 준선에 내린 수선의 발을 각각 C, D라 하자. $\rm \overline{AF}=2,$ $\rm \overline{BF}=5$ 일 때, 사각형 ABCD의 넓이는?  |
[풀이]
$$ (2+5) \sqrt{2\times5}=7\sqrt{10}$$
| Example 2 |
그림과 같이 포물선 $y^2 =12x$ 와 점 F$(3, 0)$ 을 지나는 직선이 서로 다른 두 점 P, Q에서 만난다. 두 점 P, Q에서 직선 $x=-3$ 에 내린 수선의 발을 각각 R, S라 하고 $\rm \overline{PF}=12$ 일 때 사다리꼴 PRSQ의 넓이는? 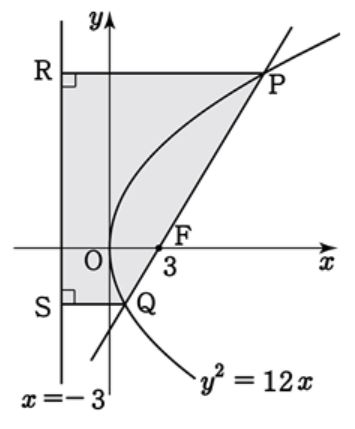 |
[풀이] $\rm \overline{QF}$ $=b$ 라 하면
$3(12+b)=12b$ 에서 $b=4$
따라서 사다리꼴 PRSQ의 넓이는
$ (12+4) \sqrt{12\times4 }=64\sqrt{3} $
728x90
'이차곡선' 카테고리의 다른 글
| 독특한 이차곡선의 접선의 방정식 (0) | 2022.08.03 |
|---|---|
| 포물선의 초점을 지나는 직선의 성질 5 (0) | 2022.07.18 |
| 포물선의 초점을 지나는 직선의 성질 3 (0) | 2022.07.18 |
| 포물선의 초점을 지나는 직선의 성질 2 (1) | 2022.07.18 |
| 포물선의 초점을 지나는 직선의 성질 1 (1) | 2022.07.17 |