728x90
합성함수에서 평균값 정리의 직관적 이해
평균값 정리는
함수 $f(x)$ 는 닫힌구간 $[a, \;b]$에서 연속이고
열린구간 $(a, \;b)$에서 미분가능할 때
$$\displaystyle\frac{f(b)-f(a)}{b-a}=f'(c)$$
인 $c$ 가 열린구간 $(a, b)$ 에 적어도 하나 존재한다.
더 확장하여 합성함수에서 편균값의 정리를 적용해보자.
| 함수 $f(x)$ 가 닫힌구간 $\left [ \;g(x),\; h(x) \; \right]$ 에서 연속이고 열린구간 $\left [ \; g(x), \; h(x) \; \right ] $ 에서 미분가능할 때 $\displaystyle \lim_{x \to a}f(x)=\displaystyle \lim_{x \to a}g(x)=k$ 이면 $$\displaystyle \lim_{x \to a}\frac{f\left ( h(x) \right )-f\left ( g(x) \right )}{h(x)-g(x)}=f'(k)$$ |
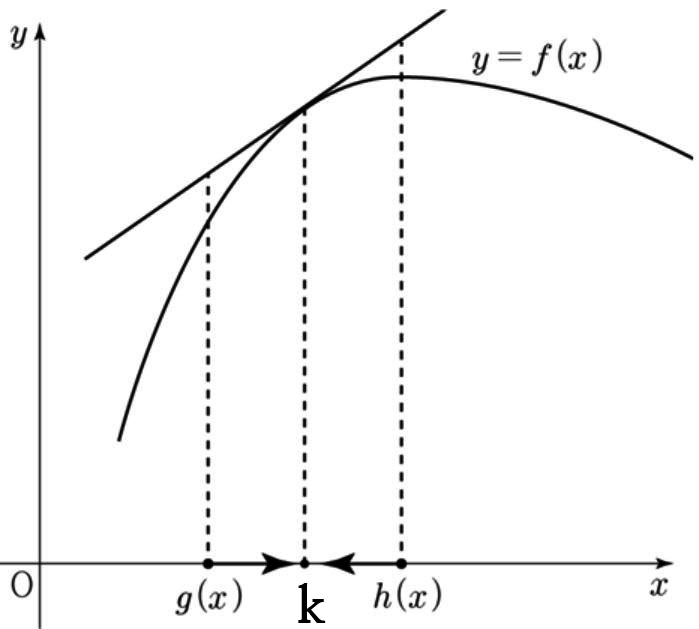
예제를 통해서 기하학적 의미를 살펴보자.
| Example 1 |
평균값 정리를 이용하여 $\displaystyle \lim_{x\to 0}\frac{e^{\tan x}-e^{\sin x}}{\tan x -\sin x}$의 값을 구하여라. |
[풀이]

$\displaystyle\frac{e^{\tan x}-e^{\sin x}}{\tan x- \sin x}$ 는 직선 $\rm {AB}$의 기울기가 나타낸다.
$x\to 0$ 한 없이 가까워져 갈수록 $\rm{AB} \to 0$이 되므로
직선 $\rm {AB}$ 의 기울기는 $x=0$ 에서의 접선기울기인 $f'(0)$에 가까워져 간다.
$$\displaystyle \lim_{x\to 0}\frac{e^{\tan x}-e^{\sin x}}{\tan x -\sin x}=f'(0)=e^0 =1$$
728x90
| Example 2 |
$\displaystyle \lim_{x \to 0}\frac{\cos (\tan x)-\cos (\sin x)}{\tan x - \sin x}$의 값은? |
[풀이] $f(x)=\cos x$ 라 하면 $f'(x)=-\sin x$ 에서
$\displaystyle \lim_{ x\to 0} \tan x = \displaystyle \lim_{ x\to 0} \sin x =0$ 이므로 $f'(0)=0$

728x90
'미분법' 카테고리의 다른 글
| 곡선 밖에서 그은 접선의 방정식 (0) | 2022.07.10 |
|---|---|
| 그래프개형 (다항함수)X(지수함수) (0) | 2022.07.09 |
| 변곡점을 갖기 위한 조건 (0) | 2022.07.08 |
| 극값을 가질 조건 (1) | 2022.07.08 |
| 극값을 갖을 조건 (0) | 2022.07.08 |