미분계수의 기하학적 의미
| 다항함수 $f(x)$ 에서 $$\frac{f^{(n)}(0)}{n!}$$ 은 $x^n$의 계수이다. |
예를 들어,
$f'(0)$ 은 일차항의 계수
$\displaystyle\frac{f''(0)}{2!}$ 은 이차항의 계수이다.
[증명]
$f(x)=a_n x^n + a_{n-1}x^{n-1}+\cdots+a_2 x^2 + a_1 x + a_0$ 라 하면
$f'(x)=na_n x^{n-1}+(n-1)a_{n-1} x^{n-1} + \cdots +2a_2 x + a_1\;\;\; \cdots \cdots ①$
$x=0$ 에 대입하면 $\therefore \;a_1 = f'(0)$
다시 ①식을 미분하면
$f''(x)=n(n-1)a_n x^{n-2}+(n-1)(n-2)a_{n-1} x^{n-3} + \cdots +2\cdot 1\cdot a_2 $
$x=0$ 에 대입하면 $f''(0)=2\cdot1\cdot a_2 $ $\therefore \;a_2 = \displaystyle\frac{f''(0)}{2!}$
일반적으로 $a_n =\displaystyle\frac{f^{(n)}(0)}{n!}$가 됨을 알 수 있다.
이를 더 일반화하면 매클로린급수가 된다.
| Example 1 |
$(x^2 + x+ 1)^6$ 의 전개식에서 $x$의 계수를 구하여라. |
[solve] $f(x)=(x^2 + x+ 1)^6$ 라 하면 $f'(x)=6(x^2 + x +1 )^5 (2x+1)$ 에서
$\therefore \;\; a_1 = f'(0)=6$
| Example 2 |
$(1+x)+(1+x)^2 +(1+x)^3 + \cdots +(1+x)^{10}$ 의 전개식에서 $x$ 의 계수는? |
[solve] $f(x)=(1+x)+(1+x)^2 +(1+x)^3 + \cdots +(1+x)^{10}$ 라 하면
$f'(x)=1+2(1+x)+(1+x)^2 +3(1+x)^2 + \cdots +10(1+x)^{9}$ 에서
$\therefore \;\; f'(0)=1+2+3+\cdots+10=55$

다항함수 $f(x)$에서 $f'(0)$ 은 $x=0$ 에서 접선의 기울기이다. $f''(0)$ 은 $x=0$ 에서 곡선의 오목 볼록을 나타낸다. |
$f''(a)>0$ 이면 함수 $f(x)$ 는 $x=a$ 에서 아래로 볼록이다.
$f''(a)<0$ 이면 함수 $f(x)$ 는 $x=a$ 에서 위로 볼록이다.
| Example 3 |
이차함수 $f(x)=ax^2 + bx + c $ 이 그래프이다. $b$ 의 계수의 부호를 조사하여라.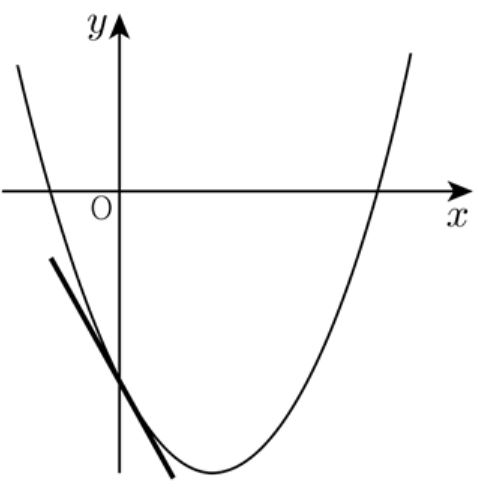 |
[solve] 중3 학생들에게는 "좌동우이" 설명한다. 대칭축이 $y$ 축 오른쪽에 있으면 $a, \;b$ 의 부호가 서로 다르다. 따라서 $b<0$이다. 미분을 이용하면 $f'(0)=b<0$ 이다.
| Example 3 |
다음 삼차한수 $f(x)=ax^3 + bx^2 + cx + d$ 의 그래프이다. $\displaystyle\frac{\left| a\right|}{a} +\displaystyle\frac{\left| b\right|}{b} +\displaystyle\frac{\left| c\right|}{c} +\displaystyle\frac{\left| d\;\right|}{d} $ 의 값을 구하여라.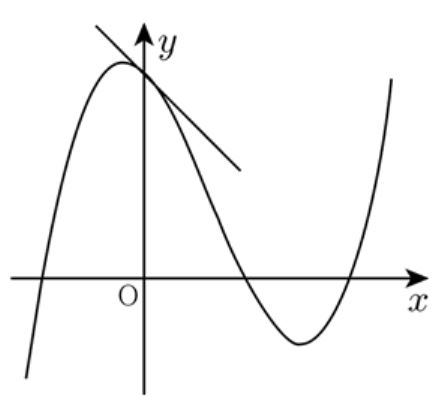 |
[solve] $a>0$ 자명
$2b=f''(0)<0$ ← $x=0$ 에서 위로 볼록
$c=f'(0)<0$ ← $x=0$ 에서 접선 기울기 음수
$d=f(0)>0$ ← $y$ 절편
\begin{align}
\displaystyle\frac{\left| a\right|}{a}& +\displaystyle\frac{\left| b\right|}{b} +\displaystyle\frac{\left| c\right|}{c} +\displaystyle\frac{\left| d\right|}{d} \\
&=\displaystyle\frac{a}{a}+\displaystyle\frac{-b}{b}+\displaystyle\frac{-c}{c}+\displaystyle\frac{d}{d} \\
&=1-1-1+1=0
\end{align}
'미분법' 카테고리의 다른 글
| 극값을 갖을 조건 (0) | 2022.07.08 |
|---|---|
| 다항함수에서 한 점에서 공통접선 | 미분가능 (0) | 2022.07.07 |
| 함수식에서 도함수 빠르게 구하기 (0) | 2022.07.06 |
| 삼차함수의 변곡점을 지나는 직선의 성질 (0) | 2022.07.05 |
| 역함수 미분 사용 설명서 (0) | 2022.07.04 |