728x90
적분의 활용 | 잘린 원기둥의 부피 | 반구에 채운 물의 부피
$$V=\frac{2}{3} r^3 \tan \theta$$
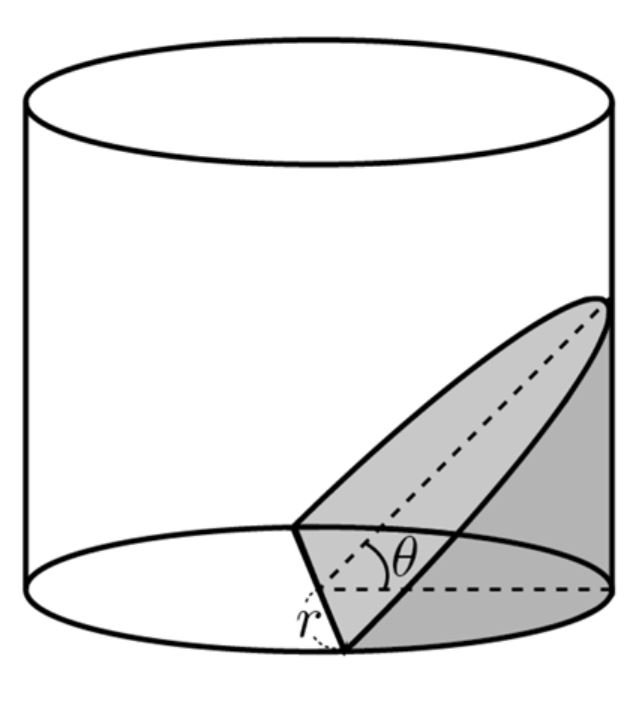
원기둥을 비스듬히 잘랐을 때 생기는 부분 중 작은 쪽은 부피를 구해보자. 대부분의 교과서와 참고서에서는 단면을 직각삼각형을 만들어서 적분으로 구한다. 단면을 직각삼각형이 아닌 여러 가지 형태로도 부피를 구할 수 있다. 이 번 포스팅에서는 직각 사각형을 만들어서 부피를 구하기로 해보자.

[증명] 원기둥의 밑면의 중심을 $O$, 밑면의 지름을 $x$축, $y$축으로 잡는다. $x$축에 수직으로 자른 단면 직사각형 $PQRS$의 넓이를 $S(x)$라 하면
$$ \overline{MN}=\overline{ON}\tan \theta =x \tan \theta, \;\; \overline {PS}=2y $$
한편, $x^2 + y^2 = r^2 $ 이므로
$$S(x)=2xy \tan \theta = 2x \sqrt{r^2 - x^2}\tan \theta $$
구하려는 부피를 $V$라 하면
$$V=\tan \theta \int_{0}^{r}2x \sqrt{r^2 - x^2}dx $$
$\sqrt{r^2 - x^2}=t$로 치환하면
$$\therefore V=\tan \theta \int_{0}^{r}2t^2 dt=\frac{2}{3}r^3 \tan \theta $$

¶ 반구 모양의 그릇에 물을 채운 후 비스듬히 기울였을 때 남아있는 물의 양을 구해보자.

$$V=\frac{\pi}{3}h^2 (3r-h)$$
증명은 각자의 몫입니다. 댓글 주시면 올려드리겠습니다.

728x90
'적분법' 카테고리의 다른 글
| 적분 점화식 정리 (0) | 2022.06.29 |
|---|---|
| 직선으로 나누어진 두 도형의 넓이의 합의 최소 (0) | 2022.06.29 |
| 수학적 귀납법 | 정적분을 이용한 증명 (0) | 2022.06.29 |
| 정적분의 활용 | 삼각함수 넓이의 이등분 (0) | 2022.06.26 |
| 적분의 활용 | 넓이가 같은 두 도형 끼워 맞추기 (0) | 2022.06.26 |