이차함수 그래프의 성질 2
이차함수 위의 두 점 A, B에서 두 접선이 만나는 점을 P 라 할 때, 직선 AB와 곡선으로 둘러싸인 영역을 T, 두 접선과 곡선으로 둘러싸인 영역의 넓이를 S라 할 때, 두 영역의 넓이 비는
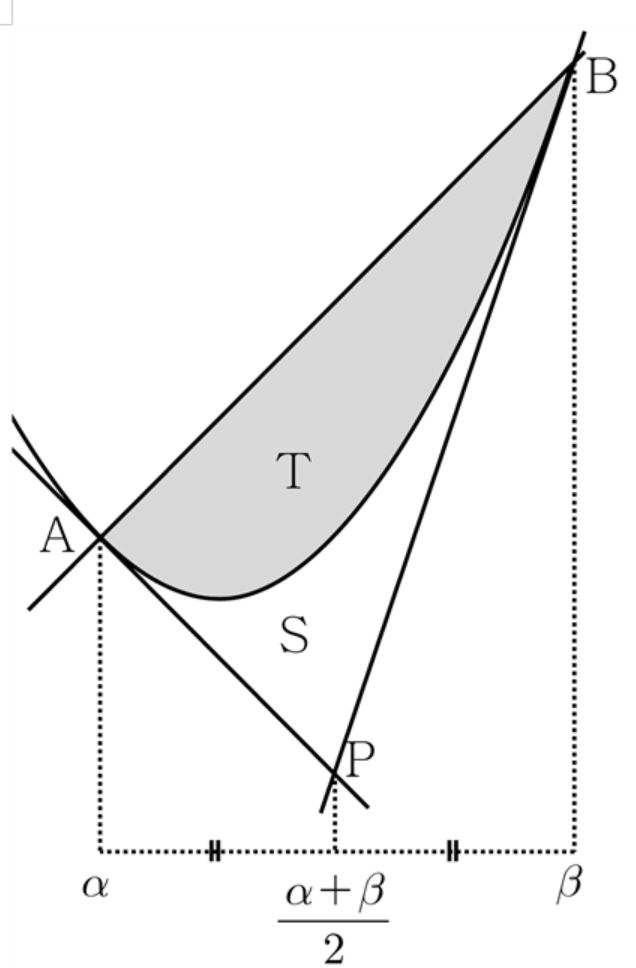
$$\rm T:S = 2:1$$ 이다.
Proof
이차함수 $f(x)=ax^2 +bx+c \;(a>0),$ 두 점 A, B를 지나는 직선의 방정식을 $g(x)$ 라 하자.
두 직선이 만나는 점을 P, 점 P에 수직인 직선이 $f(x)$ 와 만나는 점을 Q, $g(x)$ 와 만나는 점을 R이라 하면

삼각형 PAB의 넓이를 S는
$$\rm S=\frac{1}{2} (\beta-\alpha) \overline{PR}$$
점 P점의 $x$ 좌표를 $\gamma$라 하면 $\gamma=\displaystyle\frac{\alpha+\beta}{2}$ 이므로
\begin{align}
\overline{\textrm{PR}} &=2a(\gamma-\alpha)^2 \\
&=2a \cdot \frac{(\beta-\alpha)^2}{4} \\
&=\frac{a}{2} (\beta -\alpha)^2
\end{align}
한편, T 영역의 넓이는
$$\frac{a(\beta-\alpha)^3 }{6}$$이므로
S=삼각형 PAB의 넓이 $-$ T 에서
\begin{align}
\textrm{S}&=\frac{a(\beta-\alpha)^3}{4}-\frac{a(\beta-\alpha)^3}{6} \\
&=\frac{a(\beta -\alpha)^3}{12}
\end{align}
$$\therefore \; \textrm{T}:\textrm{S}=\frac{a(\beta-\alpha)^3}{6}:\frac{a(\beta-\alpha)^3}{12}=2:1$$

Example 1
곡선 $y=x^2 -4x+3$ 과 이 곡선 위의 두 점 $(0, 3), \;(4,3)$에서의 접선으로 둘러싸인 영역의 넓이를 구하여라.
[해설] 두 점을 지나는 직선과 곡선으로 둘러싸인 영역의 넓이는
$$\frac{(4-0)^3}{6}=\frac{32}{3}$$
구하는 영역의 넓이는
$$\therefore \; \frac{1}{2} \times \frac{32}{3}=\frac{16}{3}$$
'함수와 그래프' 카테고리의 다른 글
| 이차함수 그래프의 성질 1 (0) | 2022.07.24 |
|---|---|
| 함수의 대칭의 성질 3 (0) | 2022.07.23 |
| 함수의 대칭의 성질 2 (1) | 2022.07.22 |
| 함수의 대칭의 성질 1 (0) | 2022.07.21 |