포물선과 타원의 직교 조건
$$b^2 = 2a^2$$
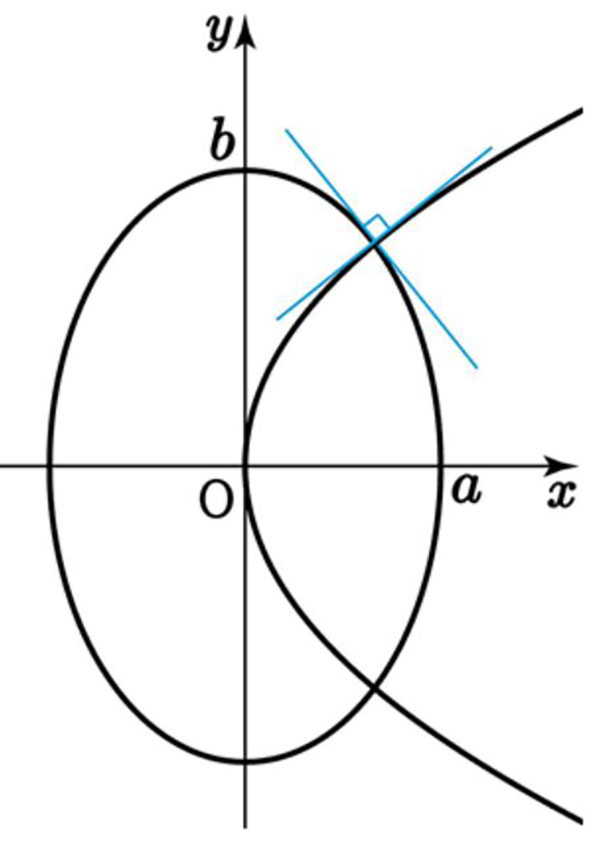
[증명] 포물선 $y^2 =4px$ 와 타원 $\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$이 제1사분면 위의 점 P에서 만날 때, 점 P의 좌표를 $\left( x_1 , y_1 \right)$ 이라 하면

점 P에서의 포물선의 접선의 방정식은 $$y_1 y = 2p(x+x_1 )$$이고 기울기는 $$\frac{2p}{y_1}$$이다.
또, 점 P에서 타원의 접선의 방정식은 $$\frac{x_1 x}{a^2}+\frac{y_1 y}{b^2}=1$$이고, 기울기는 $$-\frac{b^2 x_1}{a^2 y_1}$$이다.
교점에 P에서 두 접선이 서로 수직이므로 $$-\frac{b^2 x_1}{a^2 y_1} \times \frac{2p}{y_1} =-1 $$ $$2pb^2 x_1 =a^2 y_1 ^2$$ $$2pb^2=a^2 (4px_1)\; (\,x_1 >0,\, y_1 >0, \,p>0 \,)$$ $$\therefore \;b^2=2a^2$$
참고로 포물선의 방정식이 $x^2 = 4py$ 일 때는 $a^2 = 2b^2$ 이 된다.

Example 1
포물선 $y^2 =4x$ 와 $\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{32}=1$ 이 만나는 점에서 각각 그은 접선이 직교할 때, 상수 $a$에 대하여 $a^2 $의 값은?
[풀이] $32=2\times a^2$ $\therefore\;\; a^2 = 16$
Example 2
타원 $x^2 + \displaystyle\frac{y^2}{a}=1$ 과 포물선 $y^2 =4x$가 서로 수직으로 만나기 위한 상수 $a$의 값은?
[풀이] $a=2\times 1$ $\therefore\;\; a = 2$
'이차곡선' 카테고리의 다른 글
| 이차곡선의 기하학적 기본성질 (0) | 2022.08.18 |
|---|---|
| 타원과 쌍곡선의 접선의 성질 1 (0) | 2022.08.05 |
| 독특한 이차곡선의 접선의 방정식 (0) | 2022.08.03 |
| 포물선의 초점을 지나는 직선의 성질 5 (0) | 2022.07.18 |
| 포물선의 초점을 지나는 직선의 성질 4 (0) | 2022.07.18 |