정적분의 활용 | 넓이
| $m,\;n$이 $0$ 이상의 정수일 때 $$ I(m,n)=\int_{\alpha }^{\beta }(x-\alpha )^m (x-\beta )^n dx$$ 이라하면 $$I(m,n)=\displaystyle -\frac{n}{m+1}I(m+1, n-1)$$ 가 성립한다. |
[proof]
\begin{flalign}
I(m,n)&=\int_{\alpha }^{\beta }(x-\alpha )^m (x-\beta )^n dx \\
&=\int_{\alpha }^{\beta }\left\{ \frac{(x-\alpha )^{m+1}}{m+1} \right\}' (x-\beta )^n dx \\
&=\left [ \frac{(x-\alpha )^{m+1}}{m+1} (x-\beta )^n \right ]_{\alpha } ^{\beta } \\
& \;\;\;\;\;\; -\int_{\alpha }^{\beta } \frac{(x-\alpha )^{m+1}}{m+1} (x-\beta )^n \cdot n(x-\beta )^{n-1}dx \\
&=-\frac{n}{m+1}\int_{\alpha }^{\beta }(x-\alpha )^{m+1}(x-\beta )^{n-1}dx \\
&=\displaystyle -\frac{n}{m+1}I(m+1, n-1) &&
\end{flalign}
| 따름정리 |
| $$ \int_{\alpha }^{\beta }(x-\alpha )^m (x-\beta )^n dx =\frac{(-1)^n \; m! \; n!}{(m+n+1)!} \left ( \beta -\alpha \right )^{m+n+1} $$ |
[proof]
\begin{flalign}
&I(m,n)=\displaystyle -\frac{n}{m+1}I(m+1, n-1) \\
&=\left ( -\frac{n}{m+1} \right ) \left ( -\frac{n-1}{m+2} \right )I(m+2, n-2) \\
&=\left ( -\frac{n}{m+1} \right ) \left ( -\frac{n-1}{m+2} \right ) \cdots \left ( -\frac{1}{m+n} \right ) I(m+n, 0) \\
&=\frac{(-1)^n \; n!}{(m+1)(m+2)\cdots (m+n)}\int_{\alpha }^{\beta }(x-\alpha )^{m+n}dx \\
&=\frac{(-1)^n \; m! \;n!}{ (m+n)!}\cdot\frac{(\beta -\alpha )^{m+n+1}}{m+n+1} \\
&=\frac{(-1)^n \; m! \;n!}{ (m+n+1)!}\cdot(\beta -\alpha )^{m+n+1} &&
\end{flalign}

| Example 1 |
 이차함수 $y=ax^2 + bx + c$ 와 $x$ 축으로 둘러싸인 면적 $$\frac{\left| a\right|}{6}\left ( \beta -\alpha \right )^3$$ |
[풀이 1] 점화식 이용
$$I(1, 1)=-\frac{1}{2} I(2, 0) $$ $$=\displaystyle\int_{\alpha }^{\beta }(x-\alpha )^2 dx=-\frac{1}{2}\left [ \frac{1}{3}(x-\alpha )^3 \right ]_{\alpha } ^{\beta }$$ $$=\displaystyle-\frac{1}{6}\left ( \beta -\alpha \right )^3$$ 이차항의 계수가 $a$ 이고 넓이는 양수이므로 $$\frac{\left| a\right|}{6}\left ( \beta -\alpha \right )^3$$
[풀이 2] 오일러 적분 공식 이용
$$ \int_{\alpha }^{\beta }(x-\alpha )^1 (x-\beta )^1 dx =\frac{(-1)^1 \; 1! \; 1!}{3!} \left ( \beta -\alpha \right )^{3} $$
$$=-\frac{1}{6}\left ( \beta -\alpha \right )^3$$
| Example 2 |
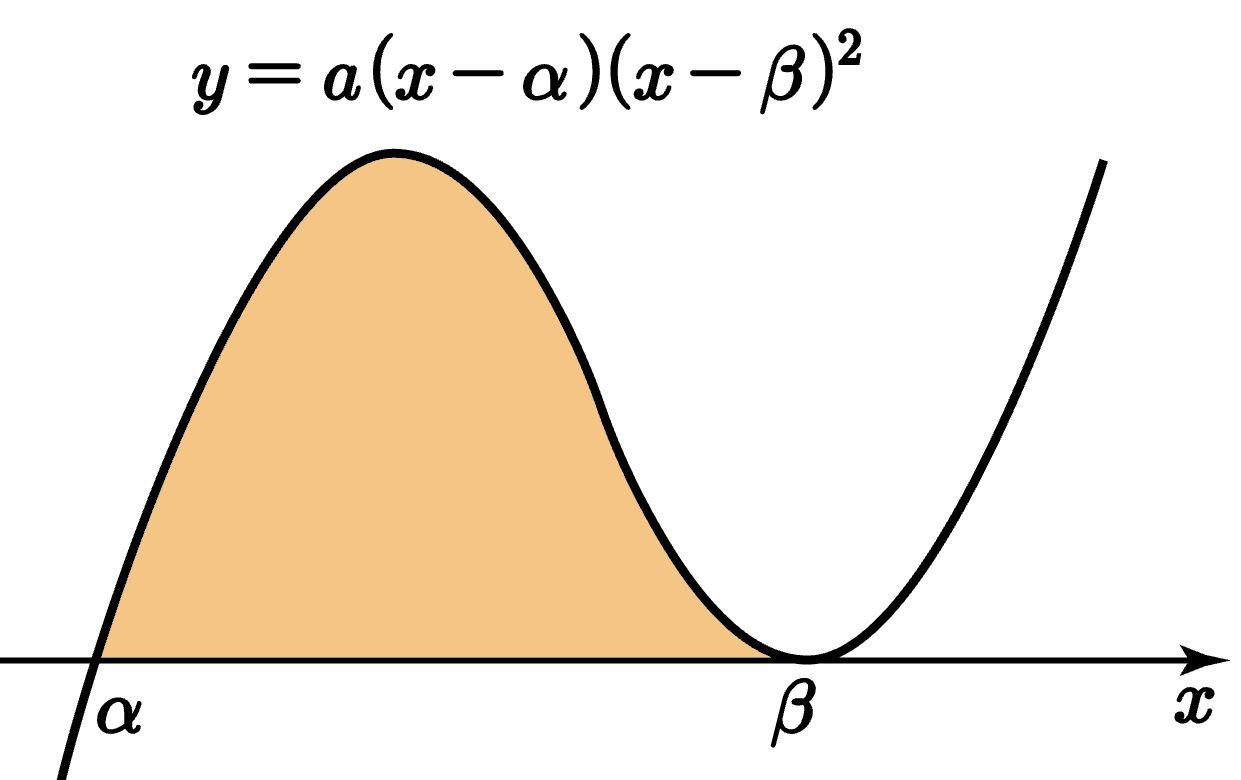 삼차함수 $y=a(x-\alpha)(x-\beta)^2$ 와 $x$ 축으로 둘러싸인 면적 $$\frac{\left| a\right|}{12}\left ( \beta -\alpha \right )^4$$ |
[풀이 1] 점화식 이용
$$I(1, 2)=-\frac{2}{2} I(2, 1) =\frac{1}{3}I(3,0)$$ $$=\displaystyle\frac{1}{3}\int_{\alpha }^{\beta }(x-\alpha )^3 dx=\frac{1}{3}\left [ \frac{1}{3}(x-\alpha )^4 \right ]_{\alpha } ^{\beta }$$ $$=\displaystyle-\frac{1}{12}\left ( \beta -\alpha \right )^4$$ 삼차항의 계수가 $a$ 이고 넓이는 양수이므로 $$\frac{\left| a\right|}{12}\left ( \beta -\alpha \right )^4$$
[풀이 2] 오일러 적분 공식 이용
$$ \int_{\alpha }^{\beta }(x-\alpha )^1 (x-\beta )^2 dx =\frac{(-1)^2 \; 1! \; 2!}{4!} \left ( \beta -\alpha \right )^{4} $$
$$=\frac{1}{12}\left ( \beta -\alpha \right )^4$$
| Example 3 |
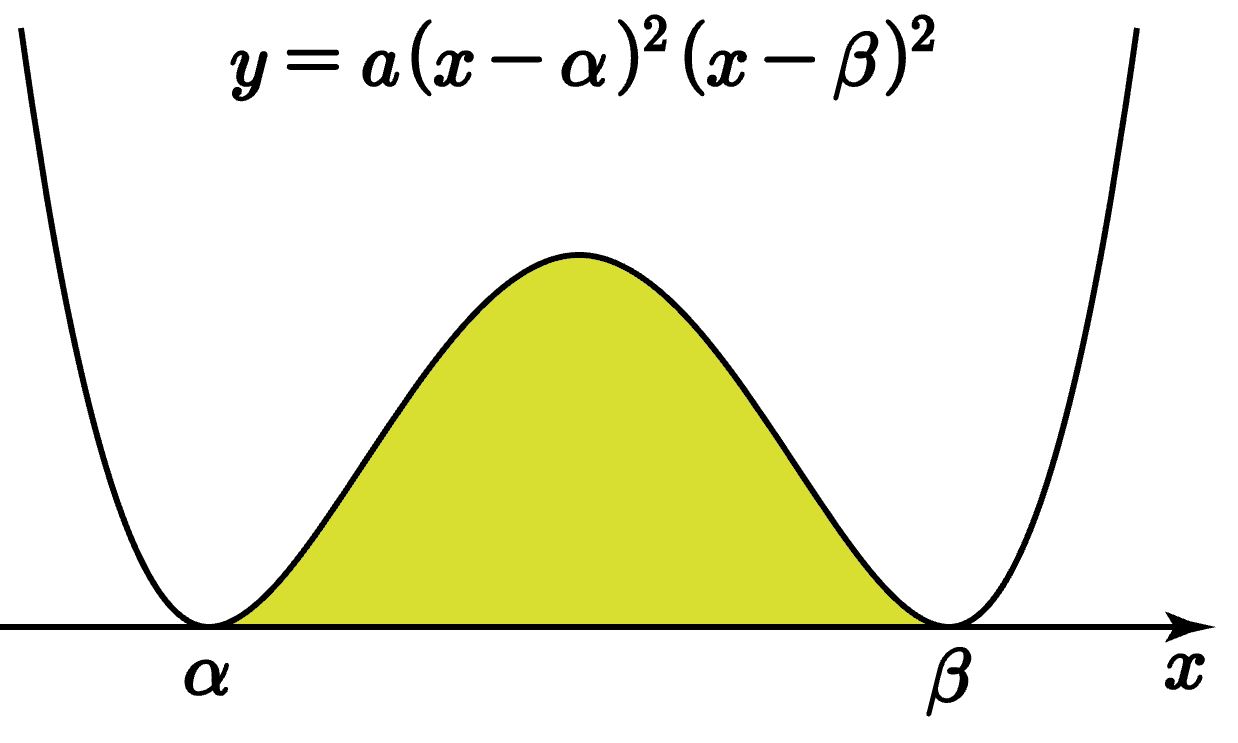 사차함수 $y=a(x-\alpha)^2 (x-\beta)^2$ 와 $x$ 축으로 둘러싸인 면적 $$\frac{\left| a\right|}{30}\left ( \beta -\alpha \right )^5$$ |
[풀이 1] 점화식 이용
$$I(2, 2)=-\frac{2}{3} I(3, 1) =\left ( -\frac{2}{3} \right) \cdot \left( - \frac{1}{4} \right) I(4,0)$$ $$=\displaystyle\frac{1}{6}\int_{\alpha }^{\beta }(x-\alpha )^4 dx=\frac{1}{6}\left [ \frac{1}{5}(x-\alpha )^5 \right ]_{\alpha } ^{\beta }$$ $$=\displaystyle-\frac{1}{30}\left ( \beta -\alpha \right )^5 $$ 사차항의 계수가 $a$ 이고 넓이는 양수이므로 $$\frac{\left| a\right|}{30}\left ( \beta -\alpha \right )^5$$
[풀이 2] 오일러 적분 공식 이용
$$ \int_{\alpha }^{\beta }(x-\alpha )^2 (x-\beta )^2 dx =\frac{(-1)^2 \; 2! \; 2!}{5!} \left ( \beta -\alpha \right )^{5} $$
$$=\frac{1}{30}\left ( \beta -\alpha \right )^5$$
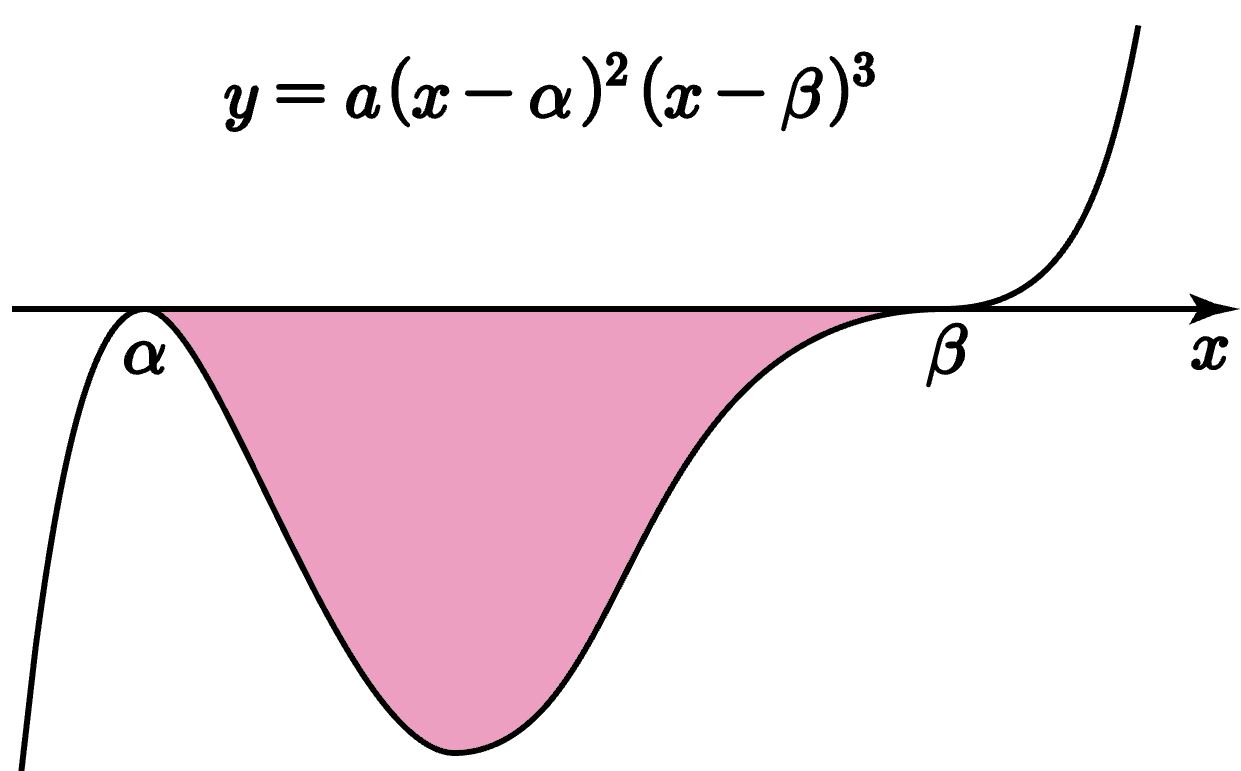
$$ \int_{\alpha }^{\beta }(x-\alpha )^2 (x-\beta )^3 dx =\frac{1}{60}\left ( \beta -\alpha \right )^6 $$
'적분법' 카테고리의 다른 글
| 삼차함수의 변곡점을 지나가는 직선의 성질 (1) | 2022.07.13 |
|---|---|
| 삼각치환을 적분 (0) | 2022.07.02 |
| 정적분을 이용한 급수의 합 구하기 (0) | 2022.07.02 |
| sin n승 cos n승 적분 점화식 | Wallis 정리 (0) | 2022.07.01 |
| 적분의 대칭성 (0) | 2022.07.01 |