기울어진 좌표계 | 사교좌표계 <1편>
평면벡터에서 기울어진 좌표 활용 안내서
좌표축은 반드시 수직일 필요는 없다. 보통 흔히 쓰는 좌표는 데카르트 좌표로 불리는 직교좌표이다. 이번 글에서는 기울어진 좌표계에 대해서 이야기해 보기로 하자.
좌표를 쓰는 이유는 어떤 점이나 물체의 위치를 표현하기 위함이다. 점의 위치를 표현하는 방법중에는 여러가지 방법이 있다. 대표적으로 많이 쓰는 좌표계에는 '직교좌표계' , ' 극좌표계', '원주좌표계', '구면좌표계' 등이 있다.
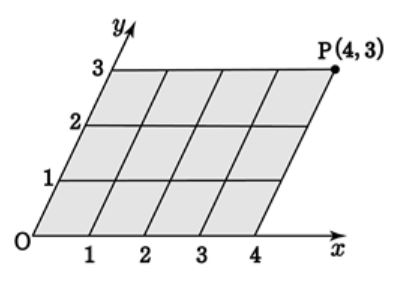
사교좌표계는 $x,$ $y$ 축이 기울어져 있는 좌표계이다. 기울어져 있었도 점의 위치를 표현하는 것은 문제 없다. 그러나 우리가 흔히 사용하는 거리, 각, 넓이는 직교좌표에서의 값을 의미하므로 사교좌표에서는 거리, 각, 넓이, 부피는 바로 사용할 수는 없다. 하지만 점들의 위치관계, 연결상태, 비율등은 변하지 않는다.
| Example 1 |
$\rm \triangle $ OAB의 변 OA를 $1:2$ 로 내분하는 점을 M, 변 OB를 $3:2$ 로 내분하는 점을 N 이라 하고, 선분 AN과 선분 BM의 교점을 P 라고 한다. $\rm \overrightarrow{OA} $ $=\overrightarrow{a} \, ,$ $\rm \overrightarrow{OB}$ $=\overrightarrow{b} $ 라고 할 때, $\rm\overrightarrow{OP}$ 를 $\vec{a}$, $\vec{b}$ 로 나타내어라.
[풀이] 적당한 점을 $(1, 0), \; (0,1)$로 잡아줍니다.(각축의 단위 벡터입니다.)
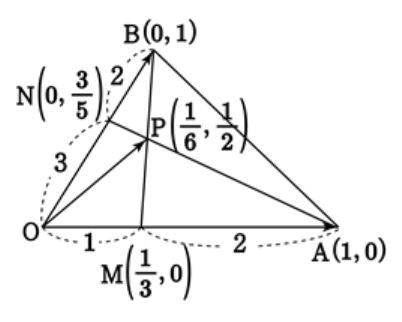
$\rm\overrightarrow{OA}$ $=(1,0)$, $\rm\overrightarrow{OB}$ $=(0,1)$ 이라 하면
$\rm\overrightarrow{OM}$ $=\left ( \displaystyle\frac{1}{3},0 \right )$, $\rm\overrightarrow{ON}$ $=\left ( 0, \displaystyle\frac{3}{5} \right )$ 이다.
직선 BM의 방정식은 $3x+y=1$
직선 AN의 방정식은 $3x+5y=3$
두 식을 연립하면
$$x=\frac{1}{6}\;\; y=\frac{1}{2}$$
$$\therefore \; \overrightarrow{\textrm{OP}}=\frac{1}{6}\vec{a} + \frac{1}{2} \vec{b}$$

| Example 2 |
한 변의 길이가 7인 정육각형 ABCDEF에 대하여 변 DE의 중점을 P, 두 선분 AP 와 BF의 교점을 Q라 할 때, 삼각형 ABQ의 넓이를 구하여라.

[풀이] 적당한 점을 원점으로 잡고 두 선분을 좌표축으로 설정해준다.
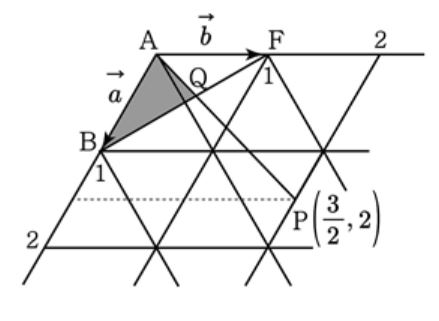
$\rm \overrightarrow {AB}=\it \vec{a}=\rm (1, 0)$, $\rm \overrightarrow {AF}=\it \vec{a}=\rm (0, 1)$ 이라 하면
놓고 직교좌표계의 성질을 이용한다.
직선 BF의 방정식은 $x+y=1,$ 직선 AP는 $4x-3y=0$ 이다. 두 식을 연립하면
$$x=\frac{3}{7}, \;y=\frac{4}{3}$$
이다. 두 직선의 교점을 Q라 하면 $$\rm Q \left ( \frac{3}{8}, \frac{4}{7} \right ) $$
$\therefore \rm \overrightarrow {AQ}$ $= \displaystyle\frac{3 \vec{a}+ 4 \vec{b}}{7} $
이다. 점 Q는 선분 BF를 $4:3$ 으로 내분한다.
\begin{align}
\triangle \textrm {ABQ} &= \displaystyle \frac{4}{7}\times \textrm{ABF} \\
&=\displaystyle \frac{4}{7} \times \frac{1}{2}\times 7^2 \times \sin 120\, ^{\circ} \\
&=7 \sqrt{3}
\end{align}