삼차함수의 비율관계 활용
삼차함수 비율관계 실전 활용
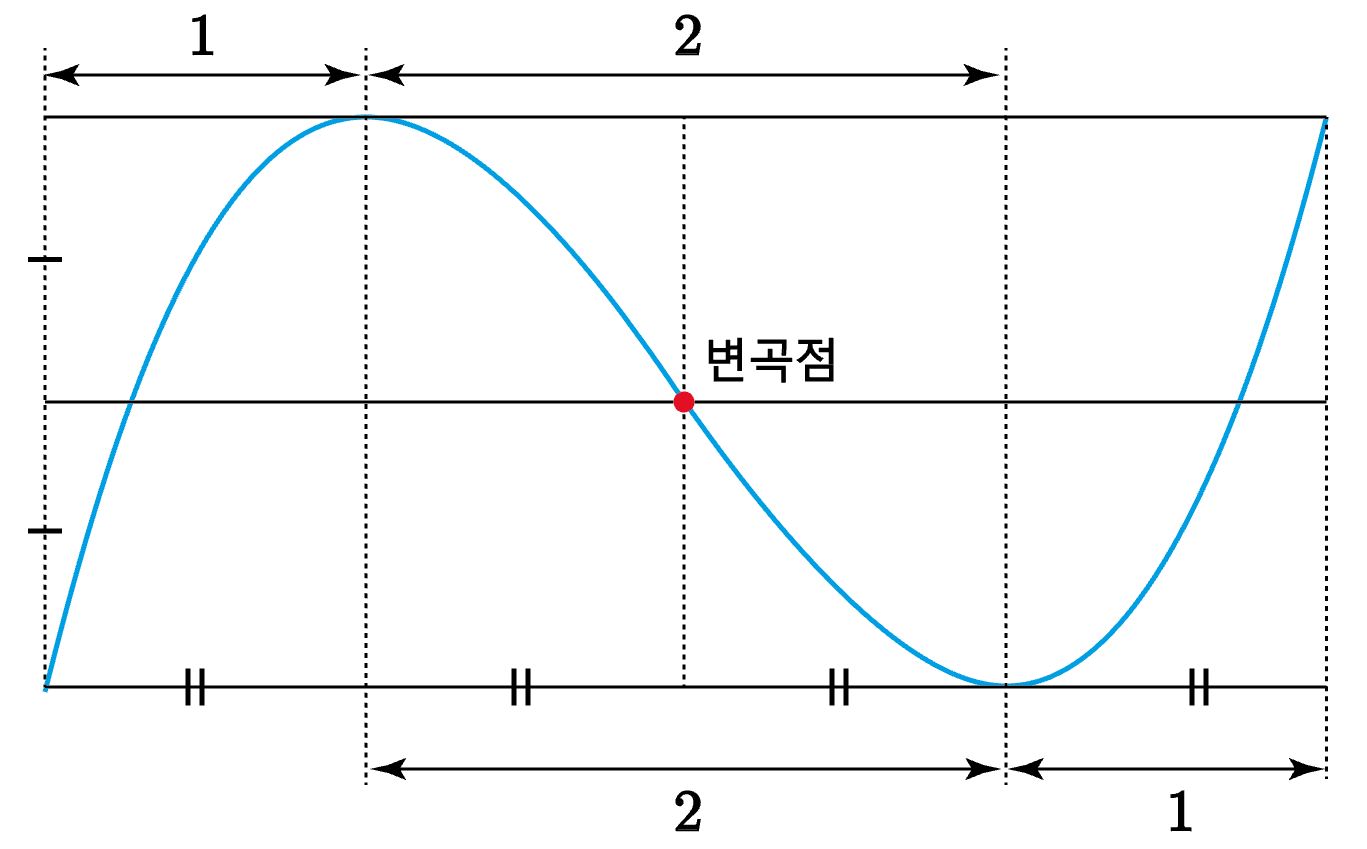

삼차함수는 변곡점에 대한 대칭이고 위의 그림과 같은 비율 관계가 성립한다. 증명은 이전 글을 참고하세요.
이번 글에서는 삼차함수의 비율관계를 실제 문제 속에서 활용하는 방법에 중점을 두기로 한다.
| Example 1 |
삼차함수 $f(x)=x^3 + ax^2 + bx$의 극댓값이 $4$ 이고 극솟값이 $0$ 일 때, $f(2)$의 값은?
[풀이]

$x=t$에서 극댓값을 갖는다고 하면 $x=3t$에서 극솟값을 가져야 한다.
$f(x)=x(x-3t)^2$ 에서 $f(t)=4t^3 =4$ $\therefore \; t=1$ $\therefore \; f(2)=2$
[다른풀이] $f(t)-4=(x-t)^2 (x-4t)$로 놓을 수 있다.
$f(0)=4-4t^3=0$ 에서 $\therefore \; t=1$ $\therefore \; f(2)=2$
| Example 2 |
$x$ 축에 접하는 삼차함수 $f(x)$ 가 있다. $f(1)=0$ 이고 $x$ 가 $2$ 에서 극댓값을 갖는다. 함수 $f(x)$ 가 $x=p$ 에서 극솟값을 가질 때, $p$ 의 값은?
[풀이] 그림을 그려보면 된다.
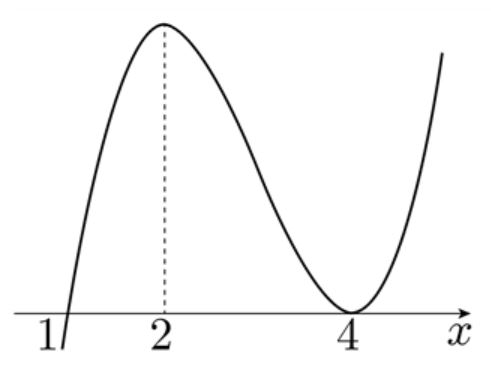
$$\therefore \; p=4$$

| Example 3 |
그림과 같이 삼차함수 $f(x)=x^3 +4x +1$ 위의 점 $ \textrm{A}(-1, 4)$ 에서 접선이 이 곡선과 다시 만나는 점을 $B$ 라 하자. 점 $P$ 가 $\textrm{A}, \textrm{B}$ 사이를 움직일 때, $\triangle \textrm{ABC}$ 의 넓이가 최대가 되도록 하는 점 $\textrm{P}$의 좌표를 구하여라.
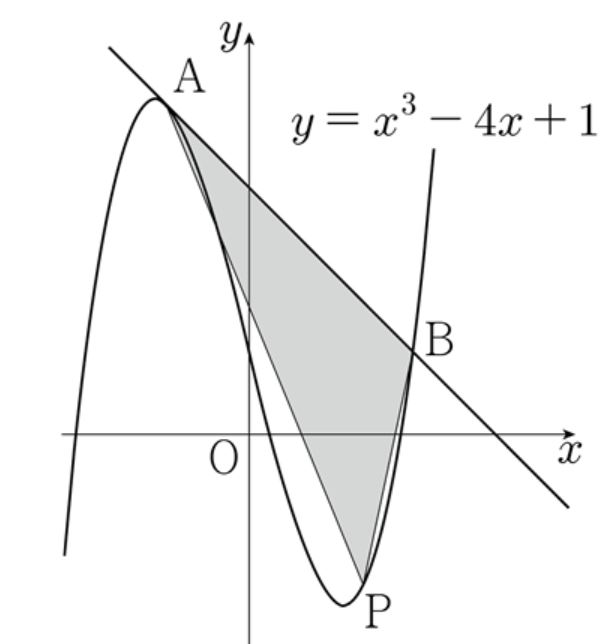
[풀이] 점 B의 $x$ 좌표를 $a$ 라 하면
$2 \times (-1) + a = 0$ 에서 $a=2$ 이다. 삼각형 APB의 넓이가 최대일 때는 점 P에서 접선의 기울기가 직선 AB 와 평행할 때이다. 직선 AB와 평행한 접선의 접점을 Q라 하면 점 Q의 $x$좌표는 두 점 A, B의 $x$ 좌표를 $2:1$로 내분한다.
$\displaystyle\frac{2\times 2 + 1\times (-1)}{3}=1$ $\therefore \; \textrm{P}(1, -2)$
| Example 4 |
함수 $f(x)=(x-1)(x^2 + ax + b)$가 $x$ 축에 접하고 극댓값이 $4$일 때, $f(5)$ 의 값을 구하여라. (단, $f'(1)\neq 0$ )
[풀이] 그림을 그린 후에 비율관계를 맞추어 본다.
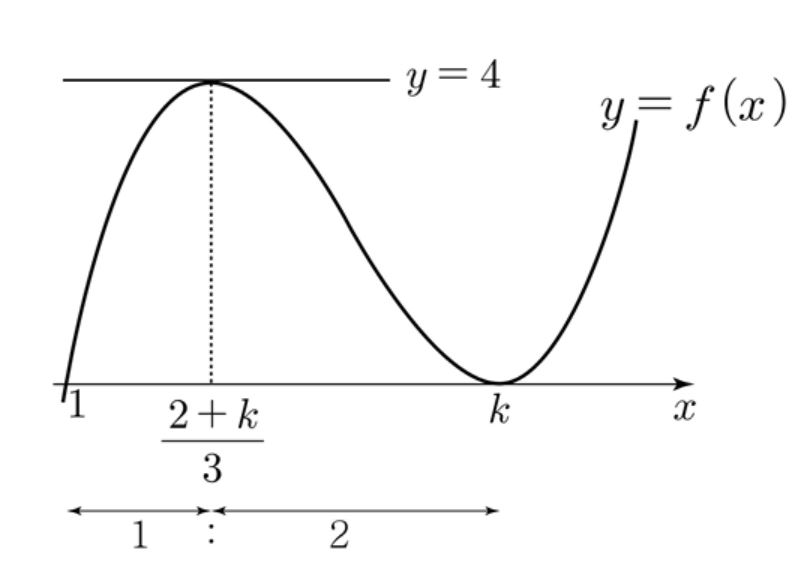
$x$ 축에 접하는 접접의 $x$ 좌표를 $k$ 라 하면
$f(x)=(x-1)(x-k)^2$ 로 놓을 수 있으므로
$x=\displaystyle\frac{2+k}{3}$ 에서 극댓값을 갖는다.
$f \left (\displaystyle\frac{2+k}{3} \right )=\displaystyle\frac{4}{27}(k-1)^3 =4$ 에서
$ k=4$ 이다. $\therefore \; f(x)=(x-1)(x-4)^2$
$\therefore \; f(5)=4$
| Example 5 |
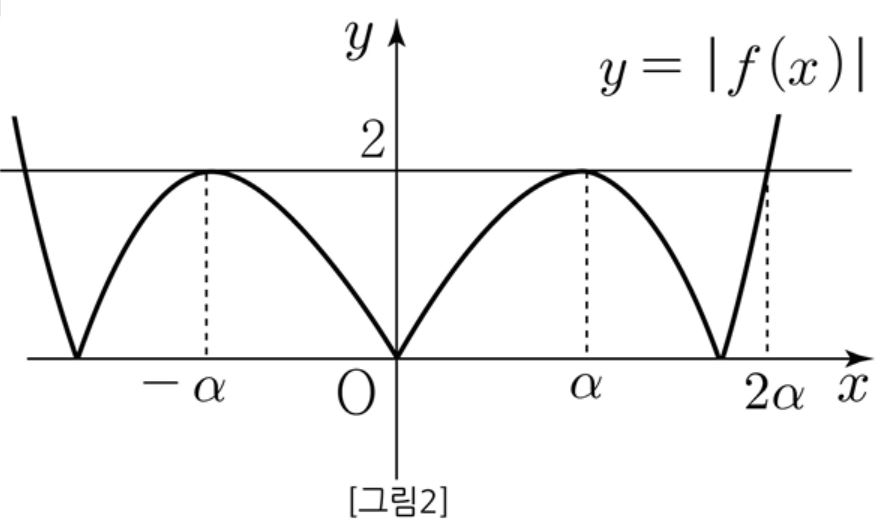
최고차항의 계수가 $1$ 인 삼차함수 $f(x)$ 가 모든 실수 $x$ 에 대하여 $f(-x)=-f(x)$ 를 만족시킨다. 방정식 $ \left | f(x) \right | =2 $ 가 서로 다른 실근의 개수가 $4$ 일 때, $f(3)$ 의 값은? [2012년 수능]
[풀이] 그림으로 문제조건에 맞게 그림을 그렴 비율관계를 이용한다.
$f(x)$ 는 기함수이므로 원정대칭이다. $x=\alpha$ 에서 극댓값을 갖는다고 하면 [그림2]에서 방정식 $ \left | f(x) \right | =2 $ 가 서로 다른 실근의 개수가 $4$가 된다.
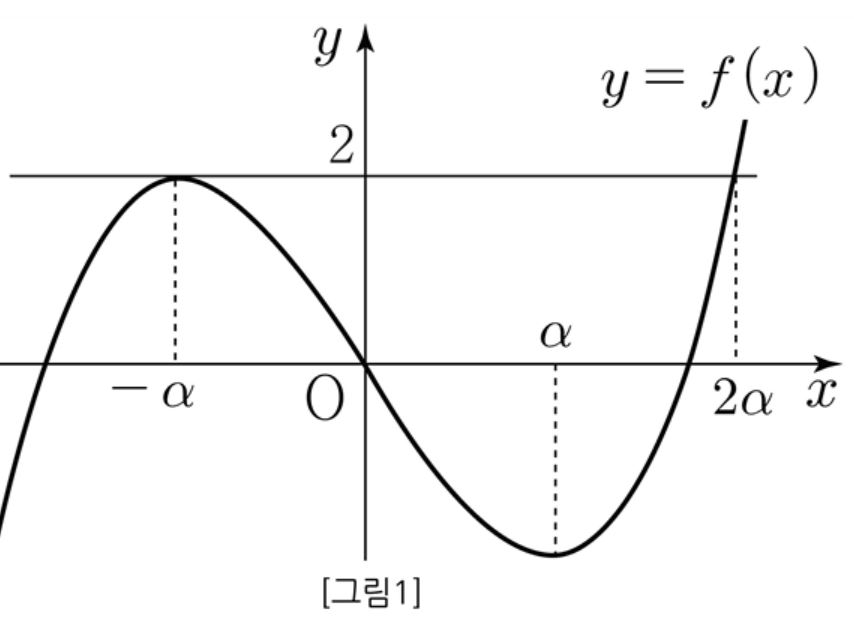
[그림1]에서 $f(x)-2=(x+\alpha)^2 (x-2\alpha)$ 가 된다.
$f(\alpha)=4\alpha ^3 \cdot (- \alpha) +2 =-2$ 에서 $\alpha =1$
$f(x)=(x+1)^2 (x-2) +2$ $\therefore \; f(3)=18$
더 많은 문제 추가 내용은 꼼수수학 수학2 를 참고하시면 됩니다.