초월함수의 극한의 근사 | 매클로린 급수
극한에서 초월함수의 근사
$x \rightarrow 0$ 일 때, $f(x) \rightarrow 0$이면 왼쪽의 함수는 오른쪽 함수로 근사된다.
| $\sin f(x)$ | $\Rightarrow$ | $f(x)$ |
| $\tan f(x)$ | $\Rightarrow$ | $f(x)$ |
| $e^{f(x)}-1$ | $\Rightarrow$ | $f(x)$ |
| $a^{f(x)}-1$ | $\Rightarrow$ | $f(x)\ln a$ |
| $\ln \left( 1+ f(x) \right)$ | $\Rightarrow$ | $f(x)$ |
| $\log _a \left( 1+ f(x) \right)$ | $\Rightarrow$ | $\displaystyle\frac{f(x)}{\ln a}$ |
| $1-\cos f(x)$ | $\Rightarrow$ | $\displaystyle \frac{1}{2} \left\{ f(x) \right\}^2$ |
| $\cos f(x)$ | $ \Rightarrow $ | $1-\displaystyle \frac{1}{2} \left\{ f(x) \right\}^2$ |
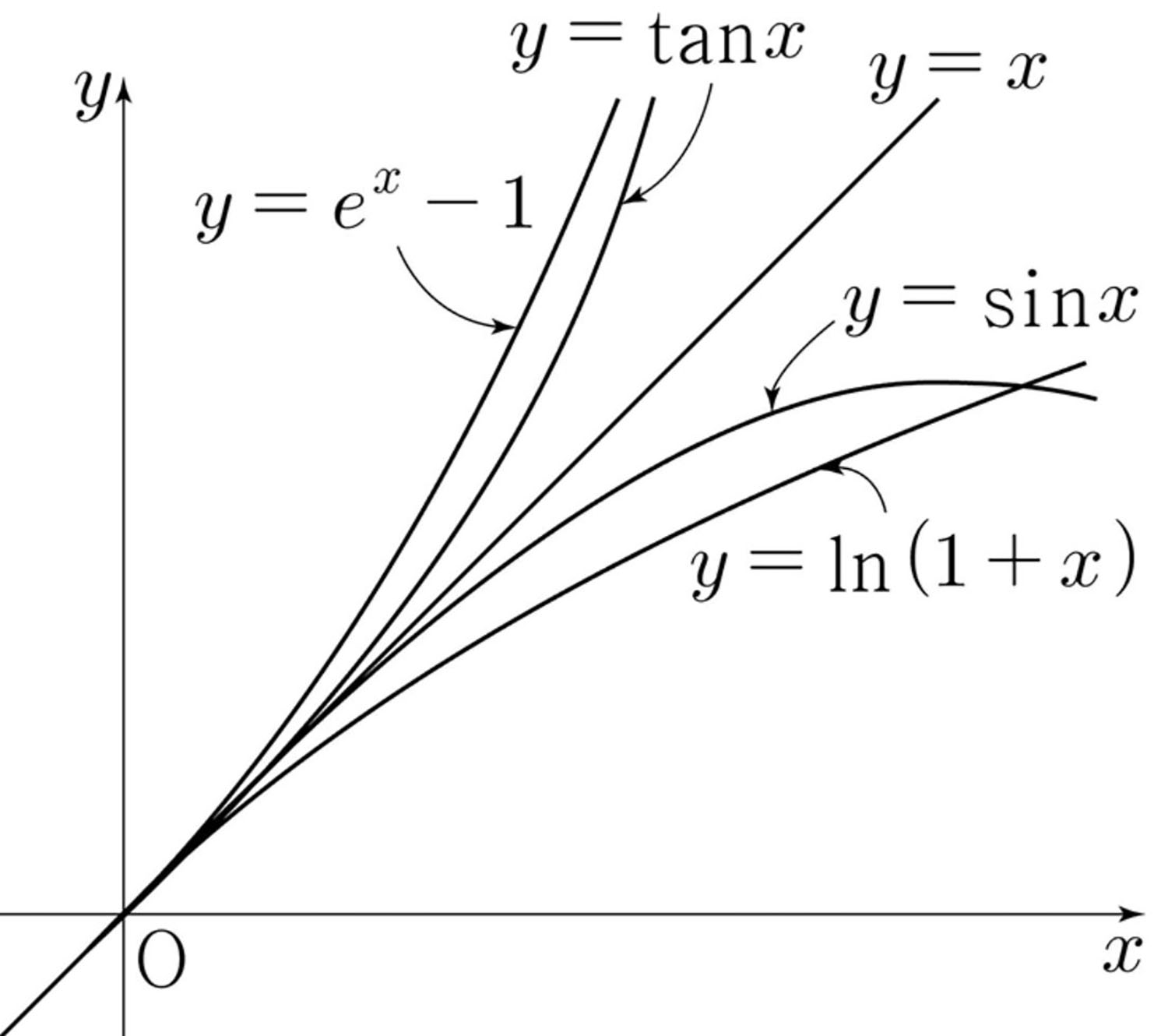
$e^x -1,\; \tan x, \; \sin x, \; \ln(1+x)$는 모두 $x=0$에서 접선기울기가 $1$이 된다.$$\lim_{x\to 0}\frac{\sin x -\sin 0}{x-0}=\lim_{x\to 0}\frac{\sin x }{x}=1$$ $$\lim_{x\to 0}\frac{\tan x - \tan 0}{x-0}=\lim_{x\to 0}\frac{\tan x }{x}=1$$ $$\lim_{x\to 0}\frac{e^x - e^0}{x-0}=\lim_{x\to 0}\frac{e^x -1 }{x}=1$$ $$\lim_{x\to 0}\frac{\ln(1+x) - \ln(1+0)}{x-0}=\lim_{x\to 0}\frac{\ln(1+x) }{x}=1$$
즉, $x\to 0$일 때는 $\sin x \to x$, $\tan x \to x$, $e^x -1 \to x$, $\ln(1+x)\to x$로 근사 시킬 수 있다.
참고로 $e^x -1$과 $\ln(1+x)$는 서로 역함수 관계이다.
Example 1
$\displaystyle\lim_{x\to 0}\frac{1-\cos x}{x \tan 5x}$ 의 값은?
[풀이] $\displaystyle\lim_{x \to 0}\frac{\displaystyle\frac{1}{2}x^2 }{x \cdot 5x}=\displaystyle\frac{1}{10}$
Example 2
$\displaystyle\lim_{x\to 0}\frac{\sin (\sin (\sin 3x))}{x}$의 극한값을 구하여라.
[풀이] 합성함수인 경우 순차적으로 근사시켜준다.
$\sin ( \sin (\sin f(x))) \to \sin(\sin f(x)) \to \sin f(x) \to f(x)$
\begin{align}
\displaystyle\lim_{x\to 0}\frac{\sin (\sin (\sin 3x))}{x}&=\displaystyle\lim_{x\to 0}\frac{\sin (\sin 3x)}{x} \\
&=\displaystyle\lim_{x\to 0}\frac{\sin 3x}{x} \\
&=\displaystyle\lim_{x\to 0}\frac{ 3x}{x}=3
\end{align}
Example 4
$\displaystyle\lim_{x\to 0}\frac{1-\cos (1-\cos 2x)}{2x^4}$의 극한값을 구하여라.
[풀이]
\begin{align}
\displaystyle\lim_{x\to 0}\frac{1-\cos (1-\cos 2x)}{2x^4}&= \displaystyle\lim_{x\to 0}\frac{1-\cos \left( \displaystyle\frac{1}{2}\cdot 4x^2 \right)}{2x^4} \\
&= \displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{1}{2}\cdot 4x^4 }{2x^4}=1
\end{align}
Example 5
[풀이]
$$\displaystyle\lim_{x\to 0} \frac{f(x)}{1-\cos (x^2)}=\displaystyle\lim_{x\to 0} \frac{f(x)}{\displaystyle\frac{1}{2}x^4}=2 $$ $$\therefore \;\; \displaystyle\lim_{x\to 0} \frac{f(x)}{x^4}=1 $$ $$p=4,\;\;q=1\;\;\; \therefore\; p+q=5$$

매클로린 급수
함수 $f(x)$가 무한히 미분가능할 때,
$$f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}+\frac{f'''(0)}{3!}x^3+ \cdot + \frac{f^{(n)}(0)x^n}{n!}+\cdots$$
가 성립한다. 이것를 이용하여 초월함수들을 다항식으로 전개할 수 있다.
| $e^x=1+x+\displaystyle\frac{x^2}{2!}+\displaystyle\frac{x^3}{3!}+\cdots$ | $\Rightarrow$ | $e^x -1 \fallingdotseq x$ | $e^x\fallingdotseq1+x+\displaystyle\frac{x^2}{2!}$ |
| $\ln(1+x)=x-\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{3}-\cdots$ | $\Rightarrow$ | $\ln(1+x) \fallingdotseq x $ | $\ln(1+x)\fallingdotseq x-\displaystyle\frac{x^2}{2}$ |
| $\sin x =x-\displaystyle\frac{x^3}{3!}+\displaystyle\frac{x^5}{5!}-\cdots $ | $\Rightarrow$ | $\sin x \fallingdotseq x$ | $\sin x \fallingdotseq x-\displaystyle\frac{x^3}{3!} $ |
| $\cos x =1-\displaystyle\frac{x^2}{2!}+\displaystyle\frac{x^4}{4!}-\cdots $ | $\Rightarrow$ | $\cos x \fallingdotseq1-\displaystyle\frac{x^2}{2!}$ | $\cos x \fallingdotseq1-\displaystyle\frac{x^2}{2!}$ |
| $\tan x =x+\displaystyle\frac{1}{3}x^3+\displaystyle\frac{2}{15}x^5 +\cdots $ | $\Rightarrow$ | $\tan x \fallingdotseq x$ | $\tan x \fallingdotseq x+\displaystyle\frac{1}{3}x^3 $ |
Example 6
$\displaystyle\lim_{x\to 0}\frac{\tan x- \sin x}{x^3}$의 극한값을 구하여라.
[풀이] $\displaystyle\lim_{x\to 0}\frac{\tan x- \sin x}{x^3}=\displaystyle\lim_{x\to 0}\frac{x- x}{x^3}\left(\displaystyle\frac{0}{0}\right)$ 다시 부정형이 된다. 1차 근사 후에도 부정형이 되면 2차 근사를 해주어야 한다. 무엇보다도 $\left( \displaystyle\frac{0}{0} \right)$ 꼴에서 벗어나야한다. 보통 이런 유형의 문제들은 식을 변형하기가 까다롭다. 또항 로피탈정리로도 큰 이득을 보지 못한다.
$\displaystyle\lim_{x\to 0}\frac{ \left( x+\displaystyle\frac{x^3}{3} \right) -\left( x- \displaystyle\frac{x^3}{6} \right) }{x^3}=\displaystyle\lim_{x\to 0}\frac{ \displaystyle\frac{x^3}{2}}{x^3}=\displaystyle\frac{1}{2}$
매클로린 급수를 활용해서 항을 추가해서 차수를 맞추어 줄 수 있다.
Example 7
$\displaystyle\lim_{x\to 0}\frac{x^2 \sin x}{3 \sin x - \sin 3x}$의 극한값을 구하여라.
[풀이]
$\displaystyle\lim_{x\to 0}\frac{x^2 \cdot x}{3 \left( x-\displaystyle\frac{x^3}{6} \right) - \left( 3x-\displaystyle\frac{(3x)^3}{6} \right)}=\displaystyle\lim_{x\to 0}\frac{x^3}{4x^3}=\frac{1}{4}$
Example 8
$\displaystyle\lim_{x\to 0}\frac{e^{2x}-1- \sin x}{x^2}$의 극한값을 구하여라.
[풀이] 분모가 2차 다항식이므로 분자도 2차 다항식으로 맞추어 준다.
$\displaystyle\lim_{x\to 0}\frac{ \left( 1+2x+\displaystyle\frac{1}{2} \cdot (2x)^2 \right)-1- x}{x^2}=\lim_{x \rightarrow 0}\frac{2x^2}{x^2}=2$